This article deals with bicycle wheel construction (the same goes for the spoked motorcycle wheels). Aiming to determine why some lacing methods and wheel designs are better than the others.
For a test on lateral stiffness, see Sheldon Brown’s “Wheel Stiffness Test.”
If you have any questions (or additions and corrections), please use the BikeGremlin forum:
www.bikegremlin.net
Table Of Contents (T.O.C.):
- Introduction – by BikeGremlin
- Spoke lacing pattern comparison study
2.1. Preamble and introduction
2.2. The Problem
2.3. The Study
2.4. The Results
2.5. Conclusion - BikeGremlin comments
- Sources
1. Introduction – by BikeGremlin
As far as I know, this study was originally done, written and published by Elvin Sullivan (at the time I’m updating this, the article is gone from the Net 🙁 ). It was then re-published on the BikeScience Facebook group by Timmi Sinamowsk (link to that version). After I posted my video on the Science Behind she Spokes on that group, Timm Sima pointed me to this study.
After having read it, I’ve concluded it pretty much aligns with my theoretical knowledge, practical experiments and measurements. I do have a few minor objections and additions to this study, that I’ve noted in the 3rd chapter of this article, after re-publishing it in its entirety, along with Timmi Sinamowsk’s excellent introduction and additional clarification for many sections of the study. I will add enumerated references to my comments within the article in square brackets, like [ 1 ], [ 2 ] – and so on – they are all listed in the 3rd chapter, and clicking on them from within the article takes you to the relevant comment.
I haven’t been able to get in touch with the author(s) to get permission or disapproval for publishing this. If anyone knows how to get in touch – please let me know.
Now, for the article:
2. Spoke lacing pattern comparison study
2.1. Preamble and introduction
Which spokes configuration transfers the most power?
Radial on the left à la Campagnolo?
Radial on the right à la Mavic?
Good-ol’ Cross-3 on both sides?
Computers for aerospace to the rescue!
Preamble: We use spoked wheels in bicycles because they are light, strong and perform well in a crosswind. Front wheels (without disc brakes) are symmetric from right to left, and do not have to transmit torque, therefore the design of spoked front wheels is fairly straightforward [ 1 ]. These days, many front wheels are radially laced, meaning that the spokes radiate straight out from the hub to the rim without crossing any other spokes.
Rear wheels (and Front wheels with disc brakes) transfer torque from the hub to the pavement. A radially-laced wheel cannot do this; in order to transmit torque, the spokes must come off of the hub flange at an angle. One group of spokes comes out at an angle opposite to the wheel rotation such that they pull the rim when you apply power to the pedals. These are called the trailing spokes; they transfer power through tension increasing. A second set of spokes, called the leading spokes, emerges from the hub at an angle in the direction of the wheel rotation, seeming to push the rim; they transfer power through decompression (tension release) – and thus, they actually do “push” the rim (this is the same force that counters a bump you hit in the road – an energy release that cancels out the energy pushing up on the rim). Static or propulsing, the leading and trailing spokes balance each-other (without them the wheel would collapse). The spokes come out at the hub flange at alternating angles, and cross each other one or more times. The number of crosses (designated 1x, 2x, 3x, etc.) depends on the number of spokes and the angle that they come out at. The ideal angle is for the spoke to arrive at the hub’s flange tangentially. This works out to cross-3 in a 32 or 36-hole hub [ 2 ], cross-2 or 3 on a 28-hole hub, and cross-3 or 4 on the older 40-hole hubs (presuming the rims are 622/700c, as smaller sizes such as 451 will typically take 1 cross less). The angle of incidence is as much dependent on the number of holes, the cross pattern, and diameters involved (except for radial lacing).
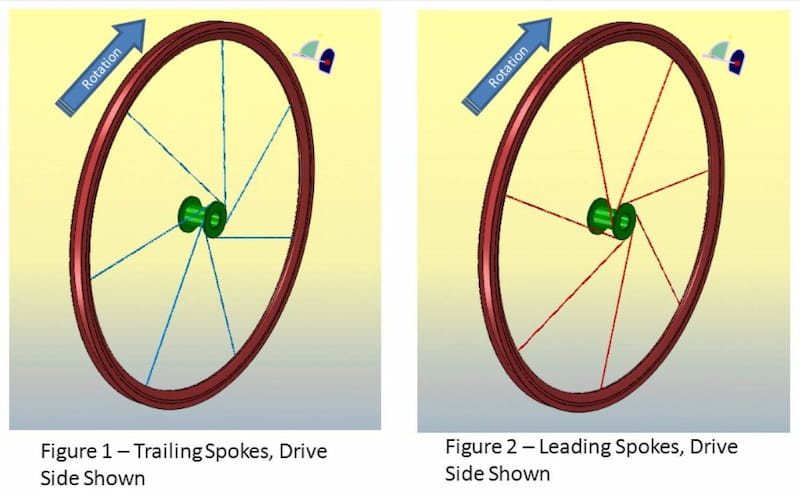
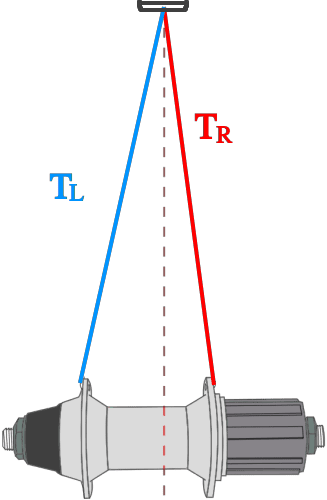
Rear wheels are further complicated by the need to accommodate the gear cluster. The freehub and cassette eat up space and force the spokes on the drive side to move closer to the wheel centerline, resulting in a dished wheel. Just as the leading/trailing spokes need to balance each other, so it is with the drive side and non-driveside spokes. Because the non-driveside spokes come in at a shallower angle, their tension is less than on the drive-side.
– BikeGremlin’s addition
Figure 2b
2.2. The Problem
When a rear wheel is tensioned, all of the drive side spokes should be at approximately the same high tension, while the non-drive side spokes should all be at some lesser tension. When power is applied to the pedals, the tension in the trailing spokes increases, while the tension in the leading spokes decreases. Because the non-drive side spokes already have a lower tension, they run the risk of becoming unloaded.
Figure 3
A wheel with spokes that become unloaded with each wheel revolution will rapidly fail. The current “quick fix” to this problem is to lace the non-drive side spokes radially (Campagnolo, Shimano, others). This decouples the non-drive side spokes from the pedal torque and takes away the problem of loss of tension on the non-drive side. Such half radial laced wheels are quite common today. Other manufacturers stick with the traditional fully crossed lacing, but make sure that the spokes have enough (pre)tension to ensure that the spokes always stay positively tensioned. One major wheel manufacturer (Mavic) goes so far as to lace the drive side spokes radially, with the crossed spokes on the non-drive side, claiming this pattern provides “optimum” energy transfer. Let’s see if this is yet another case of someone having a “bright idea” and therefore it must be so (or they know but the marketing department was in desperate want for something to set them apart from the herd).
2.3. The Study
In the face of various claims regarding spoke lacing patterns, this study set out to scientifically determine which lacing pattern builds the strongest wheel, transmitting the most power while wasting the least wattage (efficiency). To find out, we built a finite element model of a bicycle wheel and put it through a computer simulation to determine spoke tension, lateral flex and energy absorption (loss of efficiency). The model consisted of generic rim, hub and spoke components. The model began with an aluminium rim with a depth of 28 mm and width of 23 mm, typical of the current trend toward wider rims (such as Williams System 28). This was paired with a generic aluminium hub with dimensions based on the DT Swiss 240S hub. The computer model has spokes of a round cross-section with the same area as that of the popular Sapim CX-Ray spokes (the cross-section determines the strength anyways, but this eases computer modelling and simulations). For the purpose of this study, the model well represents the performance of these aero-shaped spokes. The spokes were laced to the rim in four patterns as follows:
- 3x/3x Three cross lacing on both sides
- 2x/2x Two cross lacing on both sides
- 3x/Radial Three cross lacing on drive side / Radial on non-drive side
- Radial/3x Radial on drive side / Three cross lacing on non-drive side
All of the wheels were laced with 28 spokes. But the results are expected to be directly applicable to wheels with greater or lesser numbers of spokes. In a side study, it was found that wheels with more spokes are stronger and stiffer, which comes as no surprise.
The drive side spokes were pre-tensioned to 225 pounds (100 kg-f) which stresses them to approximately 40 percent of the tensile strength of the Sapim CX-Ray spokes. The non-drive side spokes were tensioned to the lesser value of 135 pounds (60 kg-f) to balance the wheel dish. This represents a highly tensioned wheel which can be expected from a quality wheel builder using good quality components.
The wheels were loaded to simulate a straight-ahead hard pedalling effort. It is assumed that a force of 150 pounds is applied to the pedals which represents a lightweight rider fully out of the saddle standing on the pedal, or a heavier rider (such as the author) still seated in the saddle but mashing very hard. This is typical of hard climbing effort and puts maximum stress on the drive wheel. We have assumed that we are in the small ring (34T) of a compact crankset, and have selected a 22 tooth gear in the rear cassette.
We used the state of the art ABAQUS CAE finite element modelling suite to build and execute this finite element model. ABAQUS CAE is widely used in the defence, automotive and aerospace industries, and is recognized as one of the leading mechanical simulation programs on the market today
2.4. The Results
When it comes to straight-ahead power and performance, riders are concerned with lateral flex and power transfer. Because a dished wheel is asymmetric, it will distort and twist under load resulting in lateral deflections of the rim [ 3 ]. These lateral deflections are not sensed by the rider per se, but if they become large enough will result in (rim) brake rub which will spoil any rider’s effort. In addition to the lateral deflection, there are also radial and torsional (windup) deflections that contribute to the overall flexibility of the wheel. Each of these deflection components rob the rider of precious energy and reduce the wattage delivered to the pavement. Rather than get into the details of all of the deflection components, we used total strain energy absorbed by the wheel as the metric to capture the net effect of all the stiffness components. Once the strain energy absorption is known, the power loss (in watts) is calculated by multiplying the strain energy per pedal stroke by the pedalling cadence.
Structural Adequacy and Fatigue Strength
Before delving into the lateral deflections and energy loss, we must check to make sure that the wheel is structurally sound and will have a satisfactory fatigue life. The series of figures that follow show the spoke tension in the wheels after pretension, under rider weight only, and under rider weight plus pedalling effort. Spoke tension is represented in N/mm2 which is a measure of stress in the spoke material. For comparison, the tensile strength of the CX-Ray spokes is given by Sapim as 1600 N/mm2.
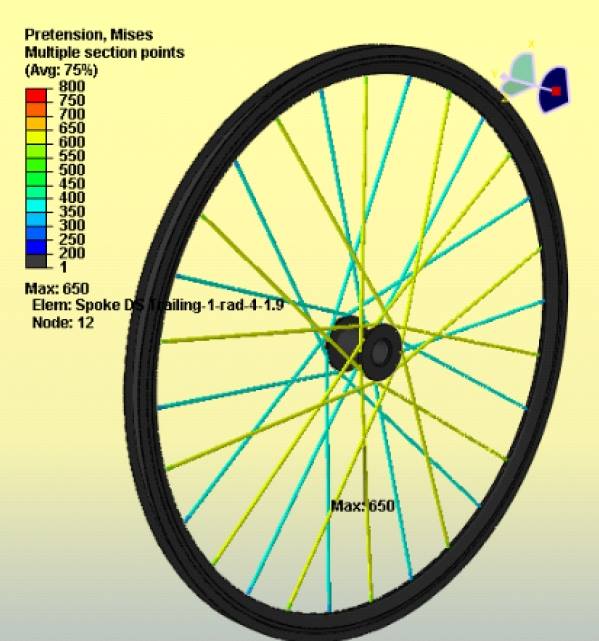
Figure 4a
The figures are shown for the 3x/3x laced wheel. In the pretension case (Figure 4a), all of the drive side spokes are evenly tensioned to 650 N/mm2, and the non-drive side spokes are tensioned to 390 N/mm2. When rider weight is added to the wheel (Figure 4b), the loads on the spokes near the bottom of the wheel are seen to decrease considerably, whereas the tension in the remainder of the spokes increases very slightly. Finally, when torque is added, the tension in all of the trailing spokes increases while the tension in the leading spokes decreases. For the 3x/3x wheel, the maximum tension was found to be 747N/mm2 on a drive-side trailing spoke, and the minimum tension was found to be 248 N/mm2 on a non-drive side leading spoke. The maximum tension is less than half of the 1600N/mm2 tensile strength of the CX-Ray spoke, which can be said to have a Safety Factor of 2.1. The minimum tension of 250 N/mm2, although significantly reduced from the original tension of 390 N/mm2, still provides a positive tension on the wheel with a generous margin of safety. The 3x/3x laced wheel is, therefore, considered structurally adequate and would be expected to have a long life without concern of spoke breakage. Results for the 2x/2x laced wheel are similar, but slightly higher (763 N/mm2 maximum, and 285 N/mm2 minimum).
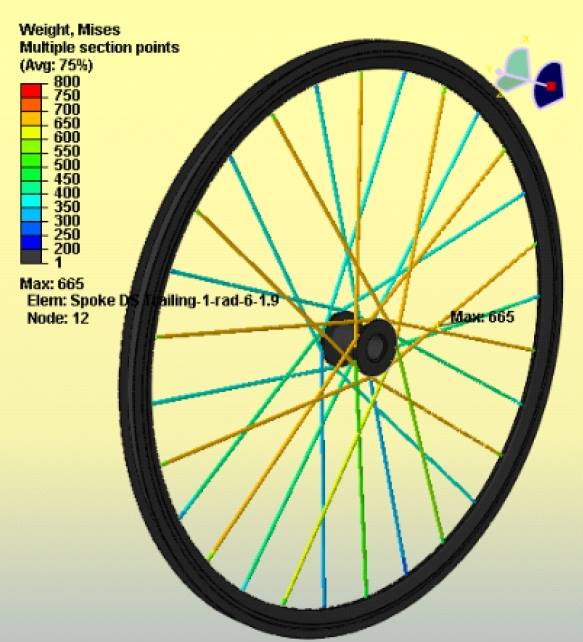
Figure 4b
Figure 5 shows the full stress plot of the 3x/3x wheel. This shows the stresses in the rim and hub, as well as those in the spokes. As can be seen, the stress in the hub and rim is much lower than in the spokes. Figure 5 demonstrates that the spoke with the least tension is a non-drive side leading spoke near the bottom. This is because (1) the non-drive side spokes have less tension to begin with; (2) Rider weight causes the spokes at the bottom to lose tension; and (3) Torque causes the leading spokes to lose tension. The figure also shows that the spokes with the highest tension are trailing spokes on the drive side away from the bottom. This is because the trailing spokes gain tension when torque is applied, and because the drive side spokes have higher tension to begin with. Note that rider weight does not have much effect once you get away from the bottom of the wheel.
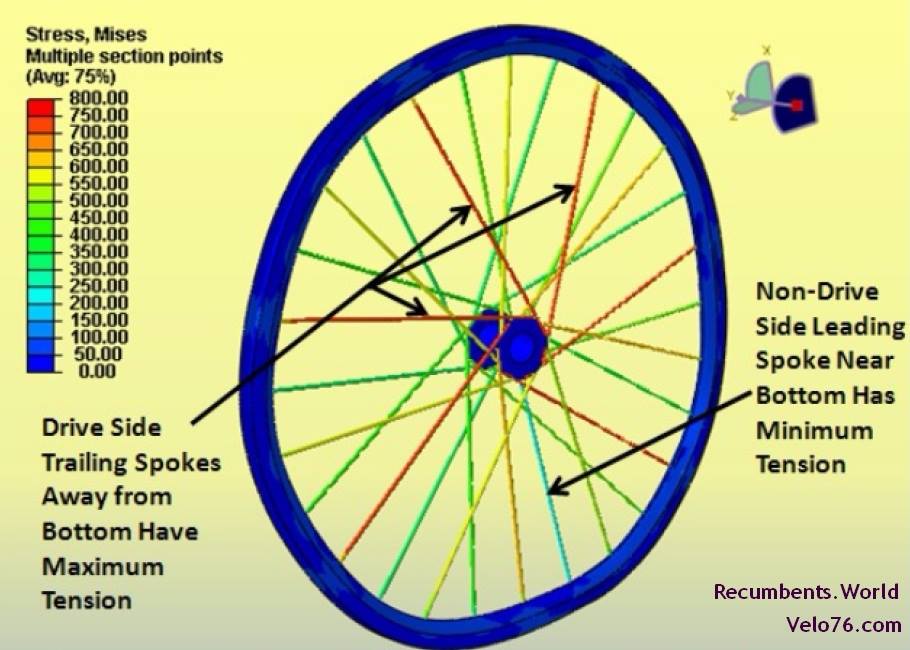
28 spokes – 3x/3x lacing
Torque plus rider weight – deflection magnified 100x
Figure 5
For the wheel with radial lacing on the non-drive side, the reduction in tension of the non-drive side spokes under torque is virtually eliminated. However, the drive side spokes experience a greater maximum tension and a greater range of tension as the wheel revolves. It is this range of tension which results in fatigue damage to the spokes and nipples.
The wheel with radial lacing on the drive side showed maximum and minimum tensions of 680 N/mm2 and 183 N/mm2, respectively. Although there is still plenty of tension on the non-drive side trailing spokes, this design provides the least margin for losing tension. The leading spokes on this wheel also go through the greatest range of tension.
Table 1 summarizes the spokes tensions in each of the wheels. The table provides maximum, minimum and maximum range of tension for the spokes.
For a wheel to be structurally adequate, the maximum tension should be well under the tensile strength of the spokes. In all four cases, we find that the tension is less than half of the tensile strength of the Sapim CX-Ray spokes. The wheel with radial spokes on the drive side has the lowest maximum tension. Perhaps, this could be advantageous if a weaker spoke material such as aluminium is used, but provides no real benefit when high strength steel spokes are used.
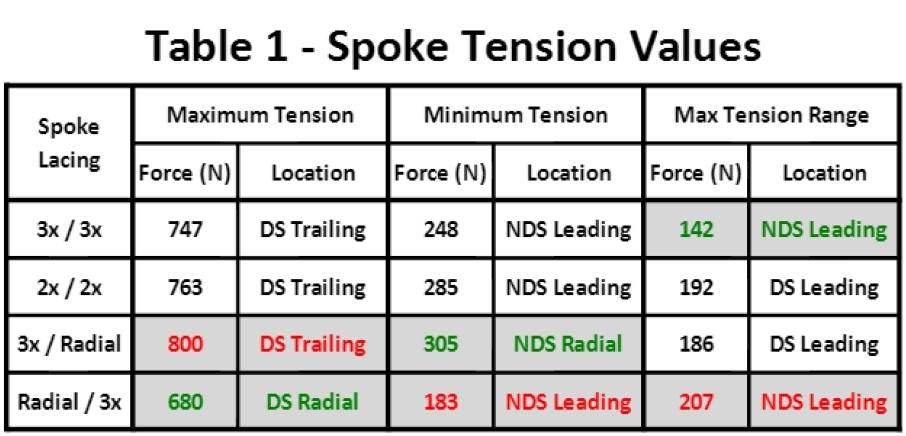
It is also desired to ensure that all spokes remain under positive tension to avoid damage to the spokes and nipples. Again all of these wheels maintain positive tension, however the Radial/3x (drive side/non-drive side) wheel has the least margin for error. Conversely, the 3x/Radial laced wheel provides the greatest margin for error. With lower tensioned spokes, the radial lacing on the non-drive side would definitely reduce the chances of losing tension, but that should not be necessary in a well built wheel with adequate pretension [ 4 ].
Tension range: Finally, and most important, is the tension range. This is the range of tension that an individual spoke will go through with each revolution of the wheel, and is the cause of metal fatigue. The design with the lowest tension range will have the longest fatigue life, and will provide the most reliable wheel. Table 1 shows that the 3x/3x wheel has the lowest tension range and would be expected to have the longest life and greatest reliability
Lateral Deflection and Brake Rub
Powerful cyclists are often concerned about brake rub during all-out climbing bursts and sprints due to flexure of the wheel. Therefore, we used the finite element models to determine the lateral deflection of the wheels under load. Figures 6 through 9 show the lateral deflection of the rim for each lacing pattern. The deflections are in millimetres.
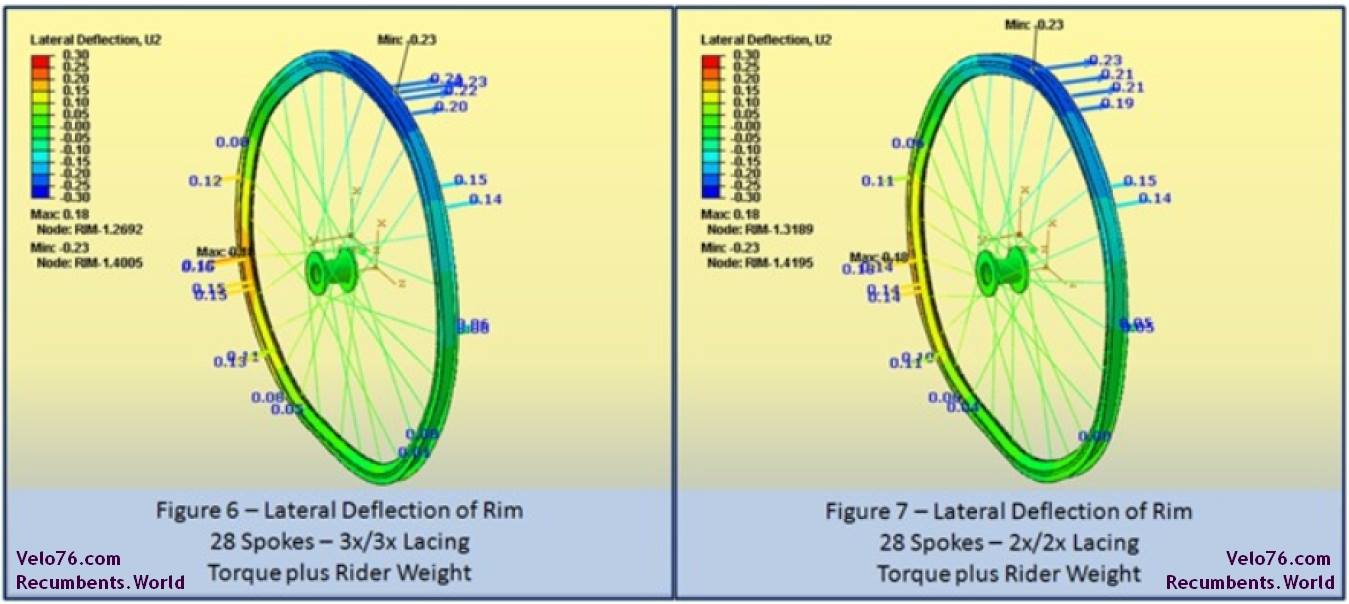
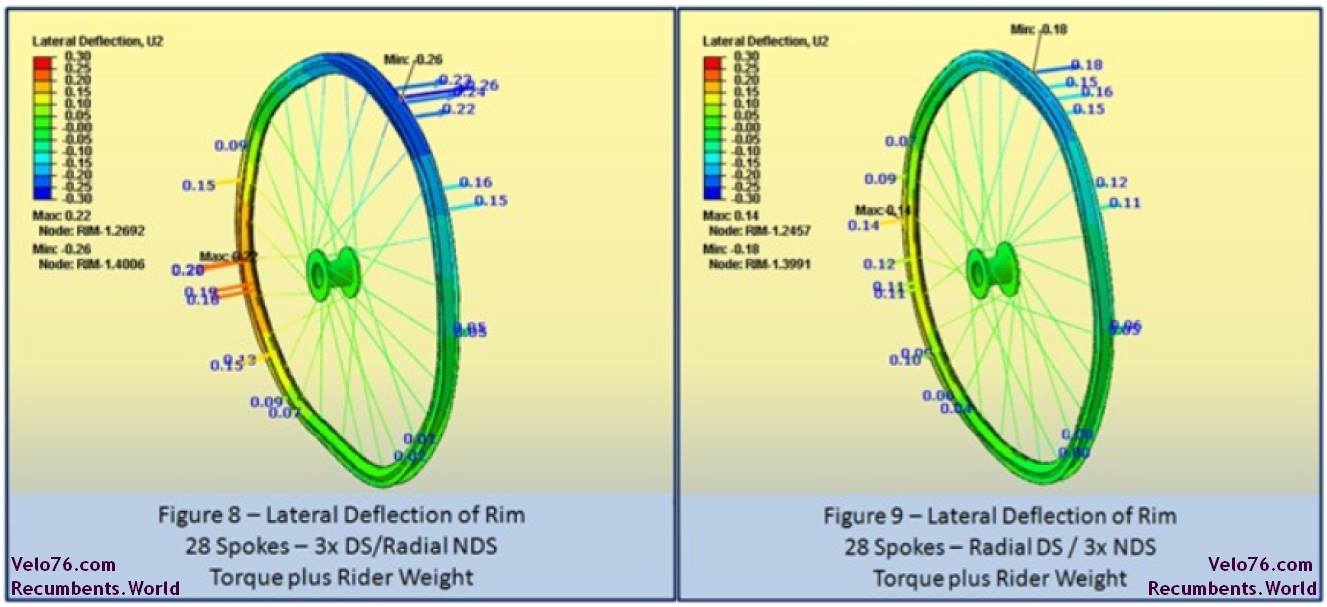
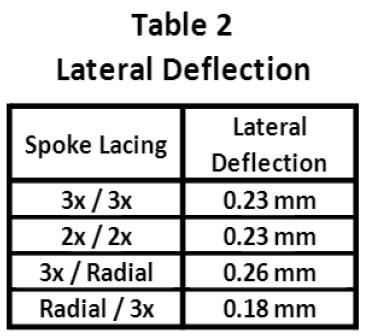
Table 2 summarizes the maximum lateral deflection of each wheel configuration. These results show that the Radial/3x (drive side/non-drive side) wheel has the least lateral deflection, and therefore the least tendency to rub the brake pads. This is somewhat surprising, since as we will show in the next section, this wheel is the least stiff overall. It appears that placing the radial spokes on the drive side provides some balance to this wheel. The 3x/Radial wheel has the greatest lateral deflection, and thus the greatest tendency to rub the brake pads. The two fully crossed wheels showed the exact same lateral deflection and fell in between the two half radial designs. All of these wheels show very small lateral deflection on the order of ¼ of a millimetre. This is likely due to the fact that these wheels all have a high spoke count. With lower spoke counts, the deflections will increase, but it is expected that the lacing trends will continue to hold [ 5 ].
General Flexibility and Power Loss
A bicycle wheel, like anything else, has a characteristic springiness which will cause it to absorb and store energy. When you push on the pedals some of your effort goes into flexing the wheel rather than being delivered to the road as useful power. This energy that is absorbed by the flexing wheel is known as elastic strain energy. It is the result of atoms in the metal grains being stretched apart. In theory, this strain energy is recoverable, but the human body does not have the capacity to recover this energy. Therefore, most of it is dissipated as heat and is wasted.
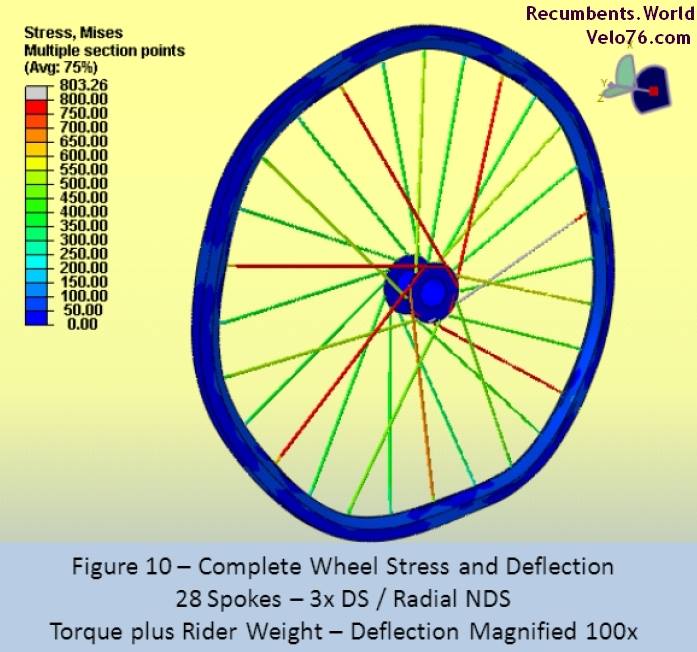
It is a principle of all springs that the stiffer the spring, the less strain energy that it will absorb under a given load. That is why bicycle frame and component manufacturers strive to make their designs very stiff (at least on the racing end of things). However, no matter how stiffly they are made, all wheels will flex to some degree under load. Refer back to Figure 5 to see the deflection of the 3x/3x wheel under torque load magnified 100 times. Figure 10 shows the similar deflection for the 3x/Radial laced wheel. Note that the half radial laced wheel deflects more than the 3x/3x wheel shown in Figure 5.
It is interesting to see how the rim tends to flatten into a polygon with seven sides. The seven sides correspond to each group of four spokes (DS Leading, DS Trailing, NDS Leading, NDS Trailing; 28/4=7).
The deflection appears dramatic in the figures because of the 100x scale factor – this is not faulty calculations, but merely a visual exaggeration for easier visualization. When viewed at a 1x scale factor, the deflection is not noticeable. Although it appears that the rim undergoes the most deflection, it is actually the stretching of the spokes that absorbs the most elastic strain energy.
Chart 1 below shows the power in watts absorbed by each of the wheels when power is applied to the pedals. The power is calculated assuming that the wheel is flexed twice per crank revolution (once for the left foot and once for the right foot). A pedalling cadence of 80 revolutions per minute is also assumed. The power is calculated as twice the strain energy divided by the time it takes to make one complete crank revolution (80 rpm -> 0.75 seconds per revolution). The value of the strain energy is calculated by the finite element analysis.
This is a simplified way to look at it. A more accurate model would be more complex, requiring a separate analysis of pressure variations in the pedal circle, as the each of the cyclist’s feet reaches different points in the pedalling circle. But this would also vary per rider, hence, it would require a vast sampling. One could assume that ours is a best-case scenario, and that there are several points in the pedalling circle where there is slightly less pressure on the pedals, multiplying the amount of times per revolution where energy losses occur.
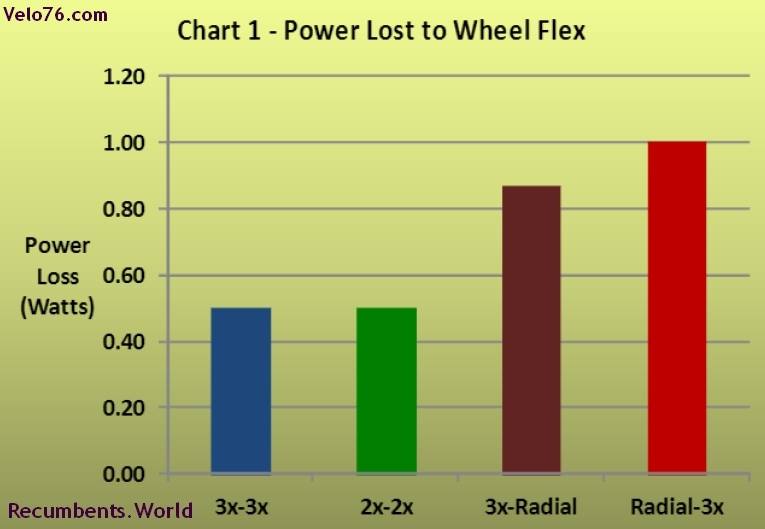
The chart shows that the fully cross laced wheels suffer significantly less power loss than the half radial laced. In fact, the 3x/3x and 2x/2x wheels lose half as much power as the Radial/3x wheel.
2.5. Conclusion
The 3x/3x wheel outperformed the two half radial wheels for two reasons: first, because all of the spokes share the power, and second, energy lost to flexing the rim (pulling it inward, especially in the radial-spokes scenarios), is not returned in a very contributing way once the rim returns to its round position.
In the half radial wheels, only the crossed spokes transfer power, the radial spokes only support the rider’s weight. Any pull (from hub-twisting within the assembly) by the radial spokes is energy lost, because none of it returns in any way to contribute to rotating the wheel. It is a simple inward and back out pull and release.
The 2x/2x wheel matched the 3x/3x wheel in stiffness and power transfer, simply because with 28 spokes on a 700c wheel, both are close to the tangential incidence angle in relation to the hub. On 32-36 spoked wheels, we can expect this difference to increase, giving the most notable advantage to the (36h) 3x/3x configuration. Given that the 3x is closest to tangential to the hub flange, the 3x/3x wheel won on fatigue strength. As the number of spokes in the wheel increases or decreases, the number of spoke crossings would need to increase or decrease to maintain the tangent condition. Accordingly, 2x lacing should be used with 20-24 spokes, 3x lacing should be used with 32 or 36 spokes, and 4x lacing should be used with 40 spokes. Although both x3 and x4 result in a near-tangential incident angle on a 36-spoke wheel, 3x is just shy of tangential, whereas 4x goes too far inwards. Indeed, depending on your wheel configuration (hub flange and rim diameter, number of spokes), the x4 sometimes crosses over onto the inside of the spoke-hole-circle, overlapping the head of the first spoke it crosses, which may cause strain and rub that could potentially compromise durability. Larger flanges will affect when the spokes become tangential with the number of crosses: they will attain that sooner, or come closer to it sooner, when the flange is larger. This however, comes at the price of less spoke length to store energy and a weight increase of the hub.
So it is concluded that the best rear wheel is cross-laced on both sides, with the number of crossings chosen to make the spokes as close to tangent to the hub flange as possible. This results in the best energy efficiency, thus, best transfer of power, AND, the most durable wheels, requiring the least frequent adjustments/alignments.
3. BikeGremlin comments
[ 1 ]
Both disc and rim brakes exert some load on the spokes. Disc brakes also exert some torque (on the front wheels as well as on the rear wheels). Noting this for clarification – no doubt that the author is aware of that (as he explicitly notes for disc brakes).
Video explanation of rim and disc braking induced spoke loads (starting at 36:38)
[ 2 ]
Here I’ve explained how to determine the optimal number of crosses. Some 36 spoked wheels can be built with a 4-cross pattern (depending on the rim and hub diameters) – making the spokes go closer to tangential, for a stronger wheel. I use this lacing pattern when building rear wheels for very heavy riders.
[ 3 ]
As far as I know, when pedalling out of the saddle, lateral loads are applied to the rim, so the flex is inevitable, regardless of whether the wheel is dished, or not. Of course, all else being equal, the more “dished” a wheel is (i.e. the wider the cassette – “more speeds”), the worse it is at handling the side loads.
[ 4 ]
Well built wheels have high enough non-drive side spoke tension – so there shouldn’t be any problems with the non-drive side spokes losing tension and going slack. Strong double-walled aluminium rims and swagged spokes help achieve this. Likewise, if spokes are laced radially, they will pivot more at the elbow, increasing the chances of hub flanges breaking from wear due to the constant movement and friction – so even though the tension decrease is reduced by radial lacing, another problem arises. Along with the problem of all the radially laced spokes trying to rip the hub flanges apart, since their pulling force acts directly away from the hub’s centre.
See this video at 13:54 for radial lacing downsides explained
[ 5 ]
Regarding the wheel flexing and rubbing the (rim) brake (or the frame for that matter – if a wide rim/narrow frame space is used):
This analysis doesn’t take any bearing play into account, but that’s not really important in this context. The biggest problem with wheel flex is how stiff the bicycle’s frame is, relative to how stiff a wheel is. Very rigid, deep-section carbon rims are notorious for rubbing. Because they don’t flex at the contact patch with the ground, but the entire (half of the) rim’s diameter acts as a lever to pull against the (rear) wheel dropouts. This causes the frame to flex and the top side of the rim to rub against the brakes.
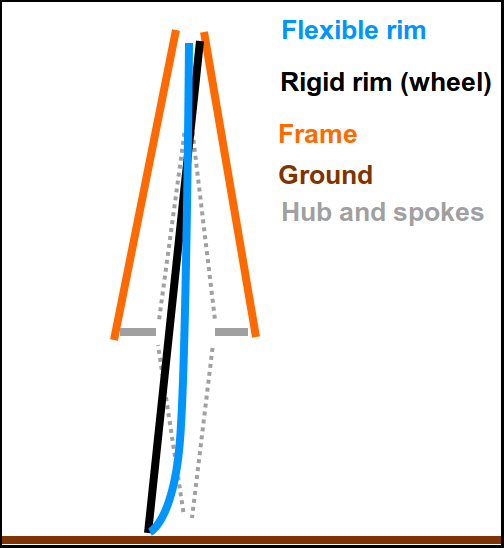
Less rigid rims (like decent strength and rigidity double-walled aluminium rims), and/or more rigid frames are of the greatest importance for preventing brake rub.
Also, for road bicycles, older style rim brakes with callipers that aren’t self-centring, and with greater pad clearance (and a bit lower mechanical advantage) can help tremendously (my video about the cons of the modern road bike caliper rim brakes).
Help BikeGremlin
stay online & independent
This website is educational, free, objective, and not commercial
(sponsors don’t enjoy paying if you mention all the product downsides that you notice 🙂 ).
How much does a WordPress website cost?
If you find this site to be good and helpful,
and if $5 per month is what you can afford to set aside,
please consider supporting my work with a Patreon donation:
4. Sources
If you have any questions (or additions and corrections), please use the BikeGremlin forum:
www.bikegremlin.net
The existing comments posted under this article (questions and answers) have been moved to this BikeGremlin forum thread:
https://www.bikegremlin.net/threads/spoke-lacing-what-makes-sense-and-what-is-nonsense-efficiency-comparison-using-advanced-engineering-software-article-comments.121/


Thank you so much for this article. Also maybe you could help, but what do you think about rims that doesn’t have holes but have steel spokes vs rims with holes and carbon spokes, what do you think should be stiffer in theory?
Hi Froust,
Stiffness depends on many different variables.
In and of itself, rims with no holes just help with tubeless tyre sealing, and make wheel building a lot more frustrating. Apart from that, all else being equal, they are not inherently stiffer (or less stiff) than the regular rims with normal spoke eyelets.
When it comes to carbon fibre – it has some awesome properties. The problem is how to tighten a spoke made of carbon fibre, without that being a weak link (some attachment and tightening system is needed), negating most of the advantages of using carbon fibre in the first place. As far as I know, it’s still not solved. Though some wheels come built with carbon spokes (i.e. spokes are built along with the rim, no way to replace a spoke or true the wheel), and such wheels can use all the advantages (and disadvantages) of carbon as a material. Too exotic and needlessly expensive for my taste. But such wheels can be very stiff, without being too heavy, nor creating too much air drag (they needn’t have a huge number of spokes).
The question is how much stiffness does one really need. Also, it would be much better and easier to just start making 7-speed (or 5-speed for that matter) hubs again. Paired with modern rear dropout spacing, such narrow cassettes would allow for some quite wide flanges, and provide a lot of lateral stiffness. But that’s not easy to sell nor make much money out of, so no one even considers it. Now, we’re on the way of adding more and more sprockets, because the marketing team of a company that couldn’t make a very good front derailleur has managed to convince consumers that front derailleurs are old-fashioned and a bad thing to have on a bike. 🙂
Relja
Hi Relja,i have built wheels using most of the patterns about for 36 and 32 spoke wheels,does not matter how you build a wheel as long as it is true,round and dished and has uniform spoke tension,i even tried lacing with the asymetrical spoke pattern,I allways go back to Roger Mussons method as that method is much easier to lace with and it runs smooth,I tried park tool method,shimano method,Sheldon Browns method and many other methods,all methods will get you a nice built wheel,if there was one standout method then every one would be lacing wheels the same way,shimano did recommend building rear disk brakes their way but did shimano ever prove their method is better?Then Sheldon said his way was better but did either back that up with technical docs?dont over think a wheel build just build that wheel the best you can using any method that works,32 or 36 spokes cross 3 fail proof pattern.If your learning to build steer clear of exotic hubs and straight pull hubs,dont forget to check your build with a spoke tension meter,make sure the rim you are using can handle the tension you end up using,if you might need to adjust the tension down the track then do it without the tire on the rim,usually a well tensioned wheel does not need touching for along time,oil or grease the spoke threads and rim holes,no need to use threadlock or locking nipples,a well build wheel does not move much at all,cheers
Hi Relja,
Thank you for the excellent article. I read it looking for information to help me decide the best pattern to use for a set of wheels I plan to build for my Bike Friday (406 wheels). These are to be for club / road riding on hopefully good roads. The wheels the bike came with are 36 hole, 3 cross. It would seem from this article, that the best choice would for me to use 2 cross rather than 3 cross:
“The ideal angle is for the spoke to arrive at the hub’s flange tangentially. This works out to cross-3 in a 32 or 36-hole hub [ 2 ], cross-2 or 3 on a 28-hole hub, and cross-3 or 4 on the older 40-hole hubs (presuming the rims are 622/700c, as smaller sizes such as 451 will typically take 1 cross less)”
Am I understanding correctly? I have noticed that when I look at the spokes as they thread into the nipples, there is a definite bend. Not huge, but visible. Again, this looks to support the 2 cross choice.
Also, is there enough difference in strength that staying with 36 hole vs either 28 or 32 matters?
Hi Rick,
The maximum number of crosses is affected by the number of holes (i.e. the number of spokes). The idea is to have spokes as close to tangential, without the spokes overlapping the adjacent spoke’s head.
My article “Bicycle wheel building basics” explains the hows and whys in more detail.
For smaller rims, the spoke entry angle (into the rim) becomes a concern. Generally, you want to keep it below 10 degrees, ideally below 7. It is not a huge issue, as you can manually bend the spoke at the rim entry point (and that is what I advise doing when building wheels, whenever needed, by pressing crossed spoke pairs towards each other).
This spoke calculator calculates the spoke entry angle:
https://www.spokelength-project.com/calculator/
Regarding the wheel’s strength: all else being equal, the more spokes, the stronger and stiffer a wheel. I see no point in building wheels with fewer than 36 spokes, unless it’s for a competition (though, even in that case, without a very good support team, I’d rather ride more reliable wheels).
Is that enough difference? For me, it is. On a 36-spoke wheel, a single spoke breaking often doesn’t even cause any rim brake rub. With 32 spokes or fewer, the wheel comes out of true enough to cause some brake rub or worse (chainstay rub or similar, depending on the particular frame, tyre width, rim stiffness etc.).
Relja