This article dives into the bicycle wheels’ rotating mass. Some cyclists think it has a huge impact on their top speed, acceleration and climbing speed. As the numbers (and my practical experience) show, rotating mass is not too important – at least when we talk about bicycles.
1. Introduction
In my article about tyre width, called Are narrower tyres “faster,” I’ve touched upon the topic of rotating mass when discussing weight (mass). There, without going into many details, I linked to a great article posted on www.biketechreview.com.
However, at the time of writing this, that website is down and the article is nowhere to be found. I had saved it, just in case. It’s a well-written article that explains the topic nicely, so I’m re-publishing it here, in order to preserve it.
So, this is not my article, I just think it’s worth sharing and preserving. I have reformated it and edited it in order to make it easier to understand (and view on a mobile for that matter).
2. Bicycle wheel performance
Sir Isaac Newton proposed his second law of motion nearly 350 years ago. This law elegantly describes the behaviour of many systems, bicycles included. It is difficult to argue with the analytical results of this equation. It is my goal to use Newton’s law to demonstrate what variables determine wheel performance and their order of significance. Furthermore, I will show how wheels rank in the big picture of overall cycling performance.
Newton declared that the sum of all the forces on a system (F) are equal to its mass (m) times its acceleration (a), or:
F = ma
Several companies offer power-measuring devices to help you quantify cycling performance. Power is defined as how much work is done during a given period of time, and it is a more convenient variable for illustrating wheel performance effects quantitatively. We can easily manipulate Newton’s law to incorporate this rider power variable. Our once simple equation now becomes:

- Aerodynamic drag resulting from
- Rider, frame, front wheel, rear wheel
- Inertial forces
- Bike and rider mass
- Front and rear wheel mass and its distribution (wheel inertia)
- Rolling resistance
- Total system mass
- Tire pressure and width
- Gravitational forces
- Bike and rider mass, front and rear wheel mass
- Miscellaneous
- Drive train losses
- Component flex
The details of this equation are beyond the scope here, so I will spare you the agonizing math (see Appendix A if that kind of stuff cranks your chain). The starred variables above are the only ones that matter when determining wheel performance. The question then becomes, which is the most important?
The obvious answer is that it’s the rider pushing the pedals that matters most. This may not be the answer you were looking for, but swapping out your wheels will not make you the next Eddy Merckx. They may, however, help out a bit in your next race.
Based on the model developed in Appendix A, and data I have collected while riding (velocity and elevation profiles), it is possible to quantify the effect your wheels have on the average power required to complete a given ride/race. I will look at the following three course examples:
- 6.5 hour solo training ride with 1200m/3940ft of climbing (31 kph/19 mph average speed from El Cajon, CA to Mexicali, B.C. Mexico)
See Appendix B for more details - The uphill portion only of the training ride above (similar to an uphill TT – 27 kph/16.8 mph average speed)
See Appendix C - 11999 Barrio Logan Grand Prix – 50 minute Pro 1,2 criterium with 10 m elevation change per lap (45 kph/28mph average speed – sitting in the pack)
See Appendix D
With my model, I varied the wheel mass, wheel inertia, and wheel aerodynamic variables independently to come up with the data in the following table:
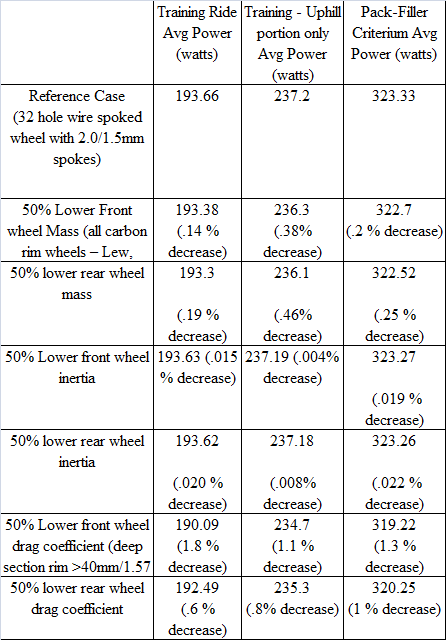
Table 1
So, what do all these numbers mean? It means that when evaluating wheel performance, wheel aerodynamics are the most important, distantly followed by wheel mass. Wheel inertia effects (i.e. “the rotating mass”) in all cases are so small that they are arguably insignificant.
How can it be that wheel inertial forces are nearly insignificant, when the advertisements say that inertia is so important? Quite simply, inertial forces are a function of acceleration. In bike racing, this peak acceleration is about 0.1 to 0.2 g’s and is generally only seen when beginning from an initial velocity of 0 (see criterium race data in Appendix D ). Furthermore, the 0.3kg/0.66lb difference in wheels, even if this mass is out at the rim, is so small compared to your body mass that the differences in wheel inertia will be unperceivable. Any difference in acceleration due to bicycle wheels that is claimed by your riding buddies is primarily due to cognitive dissonance, or the placebo effect (they paid a lot of money for the wheels so there must be some perceivable gain).
The following table illustrates how other variables in the power equation affect overall performance.
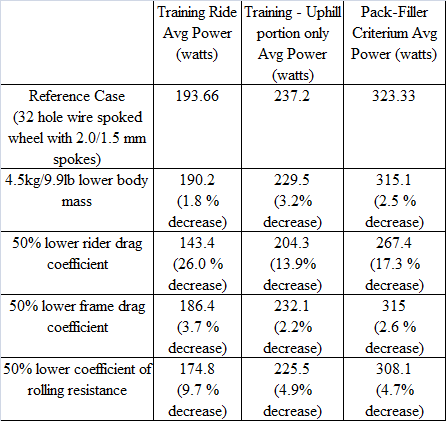
Table 2
It can be seen that rider aerodynamics dominates the power requirements of racing bikes. Frame and combined wheel effects are roughly equivalent, and it is interesting to note how power requirements are affected by rolling resistance changes in the examples.
Roughly, the average rider power requirements on a course with a zero net elevation gain is broken down into 60% rider drag, 8% wheel drag, 8% frame drag, 12% rolling resistance 0.5% wheel inertia forces and 8% bike/rider inertia. The uphill TT example given is a special case where the rider aerodynamics and the bike/rider weight have nearly equal contributions to power – somewhere around 35% each with wheel mass contributing around 1%. The steeper the hill, the more important mass becomes and the less important aerodynamics becomes. In all cases, however, there is approximately 3% of the average power unaccounted for.
Drive train losses and flexing of bicycle components can be placed into the miscellaneous term of the power equation. Even though these flexural losses are minuscule when compared to wheel inertial power requirements, lateral stiffness/deflection of wheels has its place in a performance analysis. My requirements are rather simple: road wheels should not rub brake pads during sprints and out of the saddle climbing, provided there is 2mm/0.079in of pad/rim clearance on either side. For reference, 2mm is the clearance when your dual-pivot brakes are opened up, yet they still have sufficient braking power available (BikeGremlin video on modern, road-bike dual-pivot brakes).
In summary, wheels account for almost 10% of the total power required to race your bike and the dominant factor in wheel performance is aerodynamics. Wheel mass is a second order effect (nearly 10 times less significant) and wheel inertia is a third order effect (nearly 100 times less significant). The best wheels in terms of performance are the ones that are lightweight, aerodynamic, don’t rub brake pads and are strong enough to get you to the finish line. The problem with these high-performance wheels, though, is that they sacrifice on the other two key variables important in wheel selection: durability and price. High-performance wheels are neither durable nor cheap. Nothing is ever easy, is it?


I would also be grateful of your evaluation of “aero road bikes.” It seems to me that in the past 15 or so years, there are more and more big battleship “aero road bikes” in the pro tours but, since as you point out bike drag is only 9% of the total, these new, expensive bikes are not going to help much and even more so since they do not seem to facilitate low rider drag positions.
Hi Tim,it all depends on what type of riding you do,the younger folk just love those light weight flying saucer type bikes simply because they the latest and greatest light weight bikes,they really do love those bikes,for urban riding its a different story as you need a stronger chromemoly frame bike,and you need a very durable bike that is easy to look after,urban riding is totally different to road riding as with urban riding you get cracks in concrete paths,potholes and gutters to ride over and the older steel bikes handle alot more extra weight which is what you need for urban riding,sooner or later you will be carrying a backpack or two and maybe some shopping,those racing bikes are just for that,racing and not a good choice for urban riding.then if you do bush trails you will need a different bike again,cheers
as for how aero those spaceships are you would have to put them through a wind tunnel test,just by the look of those bikes its seems they solved front on aero problems but a good cross wind would certainly slow them down
Thank you, fascinating. In your figures, I am surprised by the aerodynamic impacts from your ride “in the pack” – or does that include some time at the front of the pack too? My (limited) experience of riding in a group is that the headwind all but disappears. However, there’s another factor here, your average speeds are far higher than mine, and drag increases with the square (cube?) of the velocity – so perhaps that’s the difference?