This post explains gear inches and other measurement units for expressing effective bicycle drivetrain gear ratios.
If you have any questions (or additions and corrections), please use the BikeGremlin forum:
www.bikegremlin.net
Table Of Contents (T.O.C.):
0. History
First bicycles, called “penny-farthing”, had a direct connection of the pedals with the drive wheel.

Picture 1
With these bicycles, the gear ratio was only affected by the (huge) drive wheel diameter. So a wheel of a 60-inch diameter was faster than a 50-inch wheel but was also harder for uphill riding (and starting). Modern style bicycle (called “safety bicycle” at the time) introduced easier and safer handling, braking, with the additional “complication” of a chain drive, using (at least) two chainrings.
Then it was needed to somehow get the idea of how fast (or hard) does a new bicycle go, compared to the old one. Introducing two chainrings and a chain meant that the drive wheel diameter was no longer crucial in determining (and comparing different) gear ratios. That is where gear inch steps in.
1. Gear inch
Gear inch gives a rough estimate of how far a bicycle goes for one turn of the pedals (though not exactly, as will be explained near the end of this chapter). Gear inch units are rounded to whole numbers and have relatively low values – easy to calculate, memorize and compare. Picture 2 gives basic values that are taken into calculation.
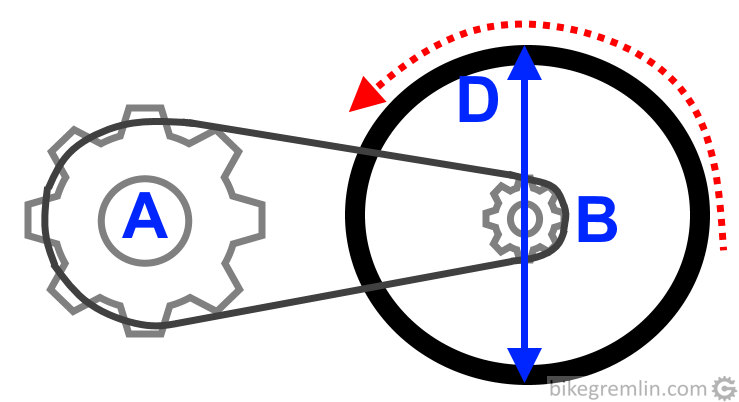
Picture 2
- A: driving chainring tooth count.
- B: rear chainring (“sprocket”, “cog”) tooth count.
- D: drive wheel diameter in inches.
- Gear inch = A/B * D.
When measuring diameter, a total diameter including the mounted tyre is taken. A wider tyre will also be “taller” and give a larger wheel diameter. The formula clearly shows that:
- The more teeth on the front chainring, compared to the rear one, the more gear inches the drivetrain will have ( A / B ).
- The larger the rear (drive) wheel diameter, the more gear inches ( * D ).
For example, if the front chainring has 50 teeth (A), the rear one has 14 teeth (B) and the rear wheel has a 28-inch diameter (D), drivetrain gear inches will be:
50 / 14 * 28 = 100 gear inches.
If we switch the rear wheel for a 26″ one, keeping the same chainrings, we’d get a gear ratio of 93 gear inches (50/14 * 26 rounded to the closest whole number).
Likewise, switching only the rear chainring for a 12 toothed one gives us 126 gear inches (50/12 * 28).
See how easy these figures are to memorize and compare? 100, 93, 126… Gear inch drive ratios rough guide is really simple:
- Up to 30 gear inches – relatively “slow”, “easy” gear ratios.
- From 30 to 70 gear inces – medium, moderately fast/slow gearing.
- Over 70 gear inches – “faster”, “harder” gear ratios.
What gear inches don’t show? The measure of how far a wheel travels for one front chainring (pedals) revolution. For that, you’d need to multiply it with the number Pi ( π ~ 3.14). Gear ratios used in examples would then be shown as:
- 100 * 3.14 = 314 inches per pedal turn ( 100 * π ).
- .93 * 3.14 = 292 inches per pedal turn.
- 126 * 3.14 = 396 inches per pedal turn.
These numbers are harder to memorize, compare and are not used in practice… not when gear inches are used. Of course, as I said in the introduction, gear inches also show what gear ratio would be achieved with a drive wheel of the given diameter in inches (as the gear inch value shows) with the cranks directly attached, using a penny-farthing design.
2. Metres of development
European, metric unit for expressing gear ratio. It is calculated similarly to gear inches, with three differences:
- Metres are used instead of inches.
- Wheel circumfence is used, instead of (just) diameter (circumfence = π * diameter).
- The value is usually rounded to one decimal place.
To use a 28″ wheel for example:
- Its diameter is 28″ * 2.54 / 100 = 0.71 metres (rounded for simplicity).
- Wheel circumfence is 0.71 * 3.14 = 2.23 m (rounded)
- Gear ratio for 50-14 chainring combination is 50/14 * 2.23 = 8.0 metres of development (rounded to one decimal).
3. What these units don’t show?
Correct time. Joking. 🙂 In terms of gear ratios, these units don’t show the total mechanical advantage. That is: when a pedal is pushed by a certain force, how much force is transferred to the drive wheel. The reason is neither of the units takes (pedal) crank length into account.
Yes, the fewer gear inches/metres of development, the more mechanical advantage, no questioning that. Still, it’s not the same whether the cranks are 165, or 175 millimetres long. It’s easier with a longer lever. This might not seem much, but it’s over 6% difference (and one of the reasons why MTB cranks are usually about 5 mm longer).
Adding the length of the cranks into the formula is not practical when comparing gear ratios (“which cassette should I get, which chainrings…”). Especially since crank length choice also depends on many other factors (desired ground clearance, rider’s leg length, pedalling style etc). So gear inches or metres of development (whichever one prefers) are good enough for comparing gear ratios and using gearing calculators to plan optimal drivetrain setup.
Help BikeGremlin
stay online & independent
This website is educational, free, objective, and not commercial
(sponsors don’t enjoy paying if you mention all the product downsides that you notice 🙂 ).
How much does a WordPress website cost?
If you find this site to be good and helpful,
and if $5 per month is what you can afford to set aside,
please consider supporting my work with a Patreon donation:
If you have any questions (or additions and corrections), please use the BikeGremlin forum:
www.bikegremlin.net

Um, a quibble: the admittedly archaic “gear inches” describe the equivalent _diameter_ of a direct drive wheel with the same mechanical advantage. Your description: ” how far a bicycle goes for one turn of the pedals” is the description if the metric “development.”
https://en.m.wikipedia.org/wiki/Gear_inches
Your formula is correct, as is the discussion of the effects.
Thanks for the feedback. 🙂
I sometimes use oversimplified, or even outright wrong explanation at the beginning, when I consider it useful for the reader to get a better understanding.
Making sure to note it and explain correctly by the end, of course.
Based on your feedback, this wasn’t very successful in this case. Will see if and how to edit the article.
So – I used a simplification for easier understanding. Perhaps not good enough. But, I wrote:
“Gear inch gives a rough estimate how far a bicycle goes for one turn of the pedals (though not exactly, as will be explained near the end of this chapter).”
And then I go on and explain it.
The article you linked to puts it better than I did:
“‘Gear inches’ is actually the diameter in inches of the drive wheel of a penny-farthing bicycle with equivalent gearing.”
Instead of what I wrote:
“gear inches also show what gear ratio would be achieved with a drive wheel of the given diameter in inches (as the gear inch value shows) with the cranks directly attached, using a penny-farthing design.”
English, not being my native, is not always easy to use as good as possible. I’m sure there are more sentences, constructions and explanations that could have been done better. So additions, suggestions and corrections are always welcome.
I think your description is clear and concise. My only suggestion is the reordering of the information. For example, put the “0.History” section towards the end of the article, and start (before any words) your article with the diagram and equations—then present your complete description.
FYI, I found your article from a Google search when looking for the definition of “gear inches.” I chose your article because a portion of the diagram appeared. I then saw the equations, which provided exactly what I needed, and then I decided to read the rest of your description.
Enjoy.
—M@
Hi Mat,
Thank you for the very constructive feedback.
I’ll seriously consider it.
To start – I think adding a table of contents at the very start of the article is a good idea.
Relja
I prefer to state bicycle gearing in inches than ratios. Easier to understand. The lower your gear inch is, the easier it is to pedal uphills. I’m more into exercise and fitness cycling than competition.
Awesome explanation of gear inches! I found the flow of the article to be interesting and concise. Thanks again. Safe riding, best wishes GMR